Introduction

Clustering serves as a foundational technique across the domains data science, machine learning, and mathematics, offering a way to uncover (that is to say ‘hidden’) inherent structures and patterns in data. In this article I consider the task of clustering a collection of vectors into groups or clusters of vectors that are close to each other, as measured by the distance between pairs of them. In particular I focus on the famous clustering method, the k-means algorithm, and give some typical applications.

The Value of Clustering

Clustering serves as a foundational technique across many domains of study, including data science, machine learning, and mathematics, offering a way to uncover inherent structures (that is to say ‘hidden’ structures) and patterns in data.

In data science, the role of applying a clustering algorithm is primarily one of exploratory data analysis. It allows practitioners to group data points into meaningful clusters based on their similarity. In turn this holds open the possibility of ‘pattern discovery’ i.e. uncovering hidden natural groupings within the data that may not have been immediately apparent otherwise.

Furthermore, clustering provides a way to segment large datasets into smaller more manageable and interpretable subsets. An example to consider here being customer segmentation within a marketing context. Once the large, unwieldly dataset has been subdivided into smaller groupings it may well be that machine learning algorithms perform better; the clustering algorithm having effectively focussed the attention of the machine learning approach. Indeed noise identification is an additional role of clustering; potentially allowing us to distinguish between significant data points versus outliers. This would be critical in studies of anomaly and fraud detection.

Finally, in feature engineering, by using a clustering algorithm as the first step in a series of predictive modelling steps, we can engineer new features by using the labels attributed to each cluster by the chosen clustering algorithm.

In machine learning, clustering algorithms are typically considered to be a type of unsupervised learning algorithm, that is, models that derive their insights from unlabeled data. As I noted just above, by applying a clustering algorithm as a preprocessing step you can create labels for the groupings found in the dataset. Such feature engineering allows you to identify data distributions, or to then apply semi-supervised learning algorithms, or to divide a larger dataset into smaller distributions each of which can be treated individually.

Clustering is also used, again as a machine learning, unsupervised, preprocessing step, for dimensionality reduction. By grouping a dataset into smaller subsets, clustering can summarize high-dimensional data into simpler representations (with fewer dimensions). Also, as part of your exploratory data analysis, you can use a clustering algorithm to help interpret complex datasets. For example, in image processing, one might wish to segment the images into specific regions. Or, in text analytics and natural language processing, a clustering algorithm can be used as part of a topic modelling study; clusters being based upon the semantic similarity of sentences for example. In fact this is precisely what I did when I presented “The Intersection of Artificial Intelligence and Ophthalmology” at XXX Congreso Boliviano de Oftalmología (see my review article here).

But the purpose and value of clustering algorithms extends to mathematics - aligning with several mathematical goals. Clustering can be used for geometric structure identification; for example helping to find relationships among points Euclidean metric space (and others) leveraging distances or similarities. In statistical modelling, clustering can represent those distributions found within datasets, such as in the case of Gaussian Mixture Models in the study of population dynamics.

Types of Clustering

Before we get into the detail of the k-means clustering algorithm lets briefly review some of the other algorithms that are popular within the data science and machine learning community.

Hierarchical Clustering

This method builds a hierarchical tree of clusters and can be subdivided into:

  • Agglomerative (bottom-up): Starts with each data point as its own cluster and iteratively merges them based on a similarity metric.
  • Divisive (top-down): Starts with all points in a single cluster and recursively splits them.
  • Strengths: Does not require predefining the number of clusters.
  • Weaknesses: Computationally expensive for large datasets.

DBSCAN

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is a density-based clustering algorithm that identifies clusters as regions of high data density separated by sparse regions. Points are classified as core points, border points, or noise based on their neighborhood density.

  • Strengths: Can find clusters of arbitrary shapes and handle noise.
  • Weaknesses: Sensitive to parameter tuning.

Mean Shift Clustering

Mean Shift is a centroid-based algorithm that iteratively shifts candidate centroids to the mean of the data points within a defined bandwidth or radius. It effectively identifies dense regions in the data.

  • Strengths: Can find clusters without predefining their number and works well for non-spherical clusters.
  • Weaknesses: Computationally intensive and sensitive to bandwidth selection.

Gaussian Mixture Models

Gaussian Mixture Models (GMM) is a probabilistic model that assumes the data is generated from a mixture of several Gaussian distributions, each representing a cluster. The model assigns probabilities to points rather than hard cluster assignments.

  • Strengths: Flexible and can handle overlapping clusters.
  • Weaknesses: Computationally expensive and may converge to a local optimum.

Spectral Clustering

Spectral Clustering uses the eigenvalues of a similarity matrix (derived from the graph representation of data) to reduce dimensionality before applying a clustering algorithm like K-Means. It is particularly effective for non-convex clusters.

  • Strengths: Works well for clusters with complex shapes and is not limited to linear separations.
  • Weaknesses: Requires a meaningful similarity graph and can be computationally intensive.

OPTICS

OPTICS (Ordering Points To Identify the Clustering Structure) is a density-based algorithm similar to DBSCAN but generates an augmented ordering of the dataset to create a reachability plot, which helps visualize the clustering structure.

  • Strengths: More robust than DBSCAN when clustering structure varies in density.
  • Weaknesses: Interpreting the reachability plot can be challenging.

Affinity Propagation

This algorithm exchanges messages between pairs of data points to identify exemplars (representative points) that define clusters. Unlike K-Means, it does not require the number of clusters to be predefined.

  • Strengths: Can find clusters of varying sizes and is less sensitive to initialization.
  • Weaknesses: Computationally expensive and can result in many small clusters.

BIRCH

BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies) is designed for large datasets and incrementally clusters incoming data points by summarizing them using a tree structure called the Clustering Feature Tree.

  • Strengths: Scales well to very large datasets and is memory-efficient.
  • Weaknesses: Assumes clusters are spherical and may not perform well with arbitrary shapes.

CURE

CURE (Clustering Using Representatives) identifies clusters by selecting multiple representative points for each cluster and shrinking them towards the cluster’s centroid to improve robustness against noise and outliers.

  • Strengths: Handles clusters of varying shapes and sizes better than centroid-based methods.
  • Weaknesses: Computationally intensive for large datasets.

The Goal of Clustering

Suppose that we have n-vectors: .

That is to say, each vector has components, and there are such vectors. In this context, the goal of clustering is to group or partition the vectors (if possible) into groups or clusters, with the vectors in each group close to each other.

Part of the task of clustering a collection of vectors is to determine whether or not the vectors can be divided into groups, with vectors in each group near each other. Of course this depends on , the number of clusters, and the particular data, i.e., the vectors .

Normally we have much smaller than i.e., there are many more vectors than there are groups. Typically applications of clustering algorithms use values of that range from a handful to a few hundred or more, where values of can range from hundreds to billions.

Toy dataset containing 500 points.
Demonstration of k-means clustering.
Toy dataset 
from sklearn.datasets import make_blobs

# X - ndarray of shape (n_samples, n_features)
#     The generated samples.
# y - ndarray of shape (n_samples,)
#     The integer labels for cluster membership of each sample.
# centers - ndarray of shape (n_centers, n_features)
#           The centers of each cluster.
#           Only returned if return_centers=True.

X, y, centers = make_blobs(
    # The total number of points equally divided among clusters.
    n_samples=500,
    # The fixed center locations.
    centers=[[-5, 3], [5, -5], [9, 9]],
    # The number of features for each sample.
    n_features=2,
    # The standard deviation of the clusters.
    # Smaller value means tighter clusters.
    cluster_std=2.0,
    center_box=(-10.0, 10.0),
    random_state=random_state,
    return_centers=True
)
k-means clustering 
from sklearn.cluster import KMeans

# Initialize the KMeans model.
kmeans = KMeans(
    # Number of clusters.
    n_clusters=3,
    # Initialization method.
    init='k-means++',
    # Number of times the k-means algorithm will
    # be run with different centroid seeds.
    n_init=10,
    # Maximum number of iterations.
    max_iter=300,
    random_state=random_state
)

# Fit the model to the data.
kmeans.fit(X)

# Get the cluster labels for each data point.
cluster_labels = kmeans.labels_

# Get the coordinates of the final centroids.
kmeans_centroids = kmeans.cluster_centers_

Illustration of a toy dataset (left) and the result of clustering with k=3 (right) using the Python scikit-learn library - modules make_blobs and KMeans respectively.

The illustration above shows a simple example, with 2-vectors, shown as small circles. We can easily see that this collection of vectors can be divided into clusters, shown on the right with the colors representing the different clusters. It may well be possible to partition these data into other numbers of clusters, but clearly is a good value.

Note of course that this example is not typical in several ways:

  • First, the vectors have dimension . Clustering any set of 2-vectors is easy - we simply create a scatter plot of our dataset and check visually if the points are clustered, and if so, how many clusters there are. In almost all applications is larger than (and typically, much larger than ), in which case this simple visual method cannot be used.
  • Secondly, the points are very well clustered. In most applications the data will not be as cleanly clustered as in this toy example; data from the real world is usually messy, with several if not many points lying in between clusters.

Even though the above example is not typical, and the best value of is not as obvious, clustering is still very useful in practice.

Common applications of clustering

Topic discovery

Suppose are word histograms associated with N documents. A clustering algorithm partitions the documents into k groups, which typically can be interpreted as groups of documents with the same or similar topics, genre, or author. Since the clustering algorithm runs automatically and without any understanding of what the words in the dictionary mean, this is sometimes called automatic topic discovery.

Patient clustering

If are feature vectors associated with patients admitted to a hospital, a clustering algorithm clusters the patients into groups of similar patients (at least in terms of their feature vectors).

Customer market segmentation

Suppose the vector gives the quantities (or dollar values) of items purchased by customer over some period of time. A clustering algorithm will group the customers into market segments, which are groups of customers with similar purchasing patterns.

ZIP code clustering

Suppose that is a vector giving quantities or statistics for the residents of ZIP code , such as numbers of residents in various age groups, household size, education statistics, and income statistics. In this example is around 40,000. A clustering algorithm might be used to cluster the 40000 ZIP codes into, say, groups of ZIP codes with similar statistics.

Student clustering

Suppose the vector gives the detailed grading record of student in a course, i.e., her grades on each question in the quizzes, homework assignments, and exams. A clustering algorithm might be used to cluster the students into groups of students who performed similarly.

Survey response clustering

A group of people respond to a survey with questions. Each question contains a statement, such as “The movie was too long”, followed by some ordered options such as Strongly Disagree, Disagree, Neutral, Agree, Strongly Agree. This is called a Likert scale, named after the psychologist Rensis Likert. Suppose the n-vector encodes the selections of respondent on the questions, using the numerical coding , , , , for the responses above. A clustering algorithm can be used to cluster the respondents into groups, each with similar responses to the survey.

Weather zones

For each of counties we have a 24-vector that gives the average monthly temperature in the first 12 entries and the average monthly rainfall in the last 12 entries. We can standardize all the temperatures, and all the rainfall data, so they have a typical range between and . The vector summarizes the annual weather pattern in county . A clustering algorithm can be used to cluster the counties into groups that have similar weather patterns, called weather zones. This clustering can be shown on a map, and used to recommend landscape plantings depending on zone.

Daily energy use patterns

The 24-vectors give the average (electric) energy use for customers over some period (say, a month) for each hour of the day. A clustering algorithm partitions customers into groups, each with similar patterns of daily energy consumption. We might expect a clustering algorithm to “discover” which customers have a swimming pool, an electric water heater, or solar panels.

Financial sectors

For each of companies we have an n-vector whose components are financial and business attributes such as total capitalization, quarterly returns and risks, trading volume, profit and loss, or dividends paid. These quantities would typically be scaled so as to have similar ranges of values. A clustering algorithm would group companies into sectors, i.e., groups of companies with similar attributes.

Clustering Objective

Let’s now formalize the clustering procedure, and introduce a natural measure of the quality of a given clustering.

Specifying the cluster assignments

We specify a clustering of vectors by stating which cluster or group each vector belongs to. We label the groups , and specify a clustering or assignment of the given vectors to groups using an N-vector , where is the group (number) that the vector is assigned to.

  • As a simple example with vectors and groups, means that:
    • is assigned to group .
    • , , and are assigned to group .
    • is assigned to group .

We also describe the clustering by the sets of indices for each group; let be the set of indices corresponding to group .

For our simple example above, we have:

Formally, we can express these index sets in terms of the group assignment vector as: which means that is the set of all indices for which .

Group representatives

With each of the groups we associate a group representative n-vector, which we denote . These representatives can be any n-vectors; they do not need to be one of the given vectors.

We want each representative to be close to the vectors in its associated group:

Note that is in group , so is the representative vector associated with data vector .

The Clustering Objective

We can now give a single number that we use to judge a choice of clustering, along with a choice of the group representatives.

We define:

which is the mean square distance from the vectors to their associated representatives. This is an “ensemble average” often referred to in statistical mechanics as a measure of the deviation of the position of a particle with respect to a reference position (and often as a function of time such that it can be updated over time). It is the most common measure of the spatial extent of random motion, and can be thought of as measuring the portion of the system “explored” by the random walker.

Note that depends on the cluster assignments (i.e., ), as well as the choice of the group representatives . The smaller is, the better the clustering.

An extreme case is , which means that the distance between every original vector and its assigned representative is zero. This happens only when the original collection of vectors only takes different values, and each vector is assigned to the representative it is equal to.

Our choice of clustering objective makes sense, since it encourages all points to be near their associated representative, but there are other reasonable choices.

  • For example, it is possible to use an objective that encourages more balanced groupings.
  • But we will stick with this basic (and very common) choice of clustering objective.

The k-Means Algorithm

The two calculations we need to solve

We have two calculations to fulfill:

  1. Choosing the group assignments.
  2. Choosing the group representatives.

Both of which are required to minimize such that, in turn, the clustering objective would be to make as small as possible.

Solving the two calculations

The two choices/calculations we need to make are circular, i.e., each depends on the other. Thus, instead of solving directly we rely on a very old idea in computation … we simply iterate between the two choices.

This means that we repeatedly alternate between updating the group assignments, and then updating the representatives. In each step the objective gets better (i.e., goes down) unless the step does not change the choice.

Iterating between choosing the group representatives and choosing the group assignments is the celebrated k-means algorithm for clustering a collection of vectors.

And so (finally!) to the k-means algorithm

The k-means algorithm was first proposed in 1957 by Stuart Lloyd, and independently by Hugo Steinhaus. It is sometimes called the Lloyd algorithm. The name “k-means” has been used since the 1960s.

In pseudocode the algorithm reads like the following:

Given: a list of N vectors x1, ..., xN, and an initial list of k group representative vectors z1, ..., zk

Repeat until convergence:

  1. Partition the vectors into k groups. For each vector i=1, …, N, assign x1 to the group associated with the nearest representative.
  2. Update representatives. For each group j=1, …, k, set zj to be the mean of the vectors in group j.

Regarding convergence, the fact that decreases in each step implies that the k-means algorithm converges in a finite number of steps.

However, depending on the initial choice of representatives, the algorithm can, and does, converge to different final partitions, with different objective values. The k-means algorithm is a heuristic, which means it cannot guarantee that the partition it finds minimizes our objective .

For this reason it is common to run the k-means algorithm several times, with different initial representatives, and choose the one among them with the smallest final value of .

Let’s create a gif animation to demonstrate the iteration of the k-means algorithm, as we’ve just defined it. First, create a toy dataset, using the make_blobs module from scikit-learn.

# X - ndarray of shape (n_samples, n_features)
#     The generated samples.

# Generate synthetic data using make_blobs
X, _ = make_blobs(
    # Effectively the number of rows in the matrix X.
    n_samples=500,
    centers=[[-5, 3], [5, -5], [9, 9]],
    # Effectively the number of columns in the matrix X.
    n_features=2,
    cluster_std=2.0,
    random_state=69,
    return_centers=False
)

Then, define a similar target for k-means clustering, again as we did previous. We expected there to be 3 clusters so we set n_clusters=3. We can set as many iterations as we feel is necessary with max_iter, knowing that in the code below there will be a if clause that looks for convergence. Let’s also define the locations of our centroids. These are initialized to points randomly selected from i.e. they are taken from the dataset itself.

# K-Means parameters
n_clusters = 3
max_iter = 10
plot_ranges = [[-9.5, 13.5], [-10, 14]]

np.random.seed(0)

# Randomly select 'n_clusters' unique indices from
# the range [0, len(X)) i.e. to len(X) - 1.
# False ensures that the same point is not selected more than once.
# Thus the 'n_clusters' centroid's intial positions are initialized
# to points randomly selected from X (i.e. taken from the dataset itself).
centroids = X[np.random.choice(len(X), n_clusters, replace=False)]

Initialize a list to store the results of each iteration. And thus store the initial locations of the centroids and the associated initial clustering label groupings.

# Initial assignment of points to the nearest centroid.
# This function computes for each row in 'X', the index of
# the row of 'centroids' which is closest to it.
# The default distance metric used is the Euclidean distance.
initial_labels = pairwise_distances_argmin(X, centroids)
labels_history = [initial_labels]

centroids_history = [centroids.copy()]

# Calculate intial mean square distance.
squared_distances = np.sum((X - centroids[initial_labels]) ** 2, axis=1)
mean_square_distance = np.mean(squared_distances)
print(f"Initial iteration: Mean Square Distance = {mean_square_distance}")

Iterate over the steps we defined in our pseudocode above.

# Iterate the k-means algorithm based on our pseudocode.
for iteration in range(1, max_iter):
    # Step 1: Assign points to the nearest centroid.
    labels = pairwise_distances_argmin(X, centroids)

    # Step 2: Compute new centroids.
    new_centroids = []
    for i in range(n_clusters):
        points_in_cluster = X[labels == i]
        if len(points_in_cluster) > 0:
            new_centroids.append(points_in_cluster.mean(axis=0))
        else:
            # No points assigned to this cluster, keep the centroid the same.
            new_centroids.append(centroids[i])

    new_centroids = np.array(new_centroids)

    # Calculate mean square distance
    squared_distances = np.sum((X - new_centroids[labels]) ** 2, axis=1)
    mean_square_distance = np.mean(squared_distances)

    # Check for convergence
    if np.allclose(centroids, new_centroids):
        print(f"\nConverged after {len(centroids_history) - 1} iterations.\nThe centroid positions after the {len(centroids_history)} iteration being identical to the previous iteration.")
        break

    print(f"Iteration {iteration}: Mean Square Distance = {mean_square_distance}")

    # Reassign points to the nearest centroid.
    # The new centroids and labels should only be appended to their respective histories if
    # convergence has not been reached. This will prevent the final two entries from being identical.
    labels_history.append(labels)
    centroids_history.append(new_centroids.copy())

    centroids = new_centroids

# Ensure both histories are the same length
try:
    assert len(centroids_history) == len(labels_history)
except AssertionError:
    print(f"centroids_history:\n{centroids_history}\n")
    print(f"labels_history:\n{labels_history}\n")
    raise AssertionError(f"Length of centroids_history ({len(centroids_history)}) and labels_history ({len(labels_history)}) do not match.")
else:
    # Check if the final two entries of 'centroids_history' are identical.
    if np.array_equal(centroids_history[-1], centroids_history[-2]):
        print("The final two entries of 'centroids_history' are identical.")
    # Likewise for 'labels_history'.
    if np.array_equal(labels_history[-1], labels_history[-2]):
        print("The final two entries of 'labels_history' are identical.")

Plot the result, step by step, to a gif.

# Create animation
fig, ax = plt.subplots(figsize=(10, 10))

def init():
    ax.clear()
    ax.set_xlim(plot_ranges[0])
    ax.set_ylim(plot_ranges[1])
    ax.spines['top'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['left'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax.xaxis.set_tick_params(labelbottom=False, length=0)
    ax.yaxis.set_tick_params(labelleft=False, length=0)
    return ax,

def update(frame):
    ax.clear()
    sns.scatterplot(
      x=X[:, 0], y=X[:, 1],
      hue=labels_history[frame],
      palette="bright",
      s=40
      ax=ax,
      legend=None
    )
    ax.scatter(
      centroids_history[frame][:, 0], centroids_history[frame][:, 1],
      s=60, c='red', marker='X', edgecolor='black'
    )
    ax.set_xlim(plot_ranges[0])
    ax.set_ylim(plot_ranges[1])
    ax.set_title(f"K-Means Clustering - Iteration {frame + 1}")
    ax.spines['top'].set_visible(False)
    ax.spines['bottom'].set_visible(False)
    ax.spines['left'].set_visible(False)
    ax.spines['right'].set_visible(False)
    ax.xaxis.set_tick_params(labelbottom=False, length=0)
    ax.yaxis.set_tick_params(labelleft=False, length=0)
    return ax,

min_frames = min(len(centroids_history), len(labels_history))

ani = FuncAnimation(
  fig, update, frames=min_frames, init_func=init, blit=False
)

# Save the animation as a GIF.
ani.save(
  "kmeans_clustering_animation.gif", writer="imagemagick", fps=1
)

plt.close(fig)

Giving us the following iterative progress.

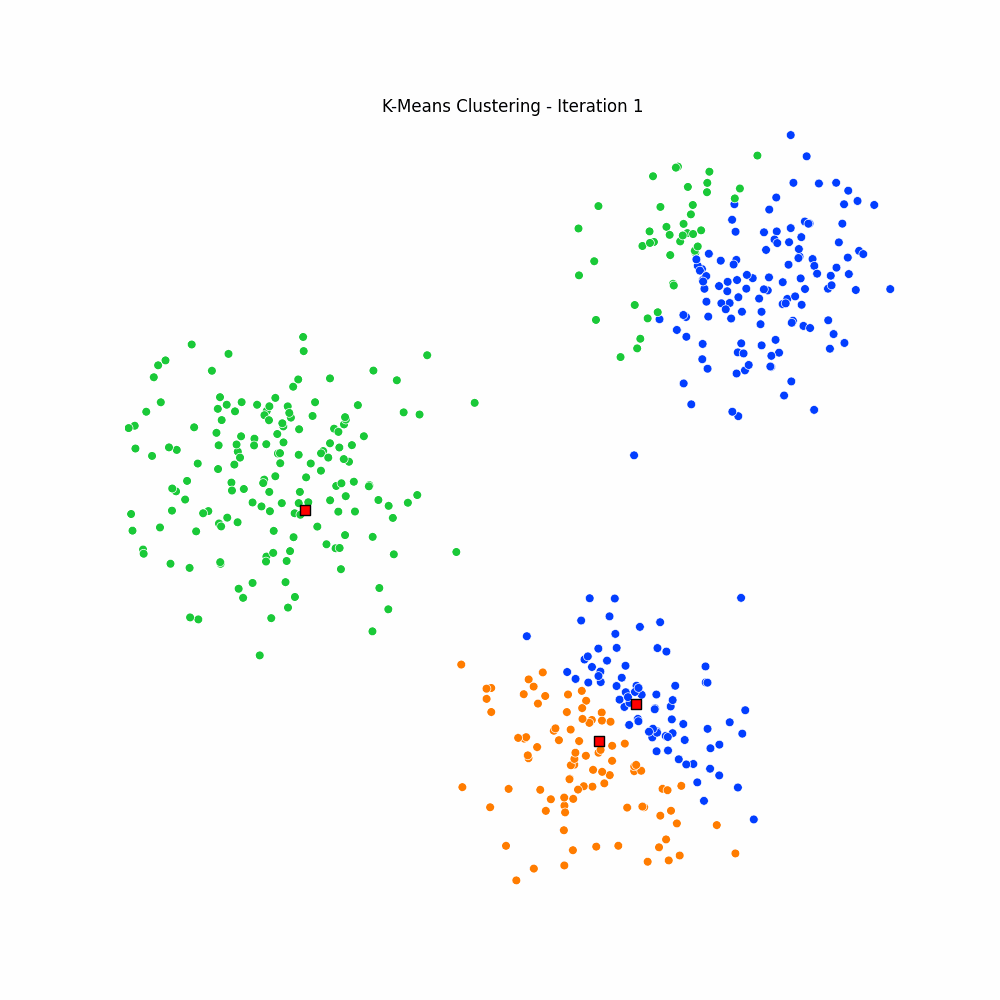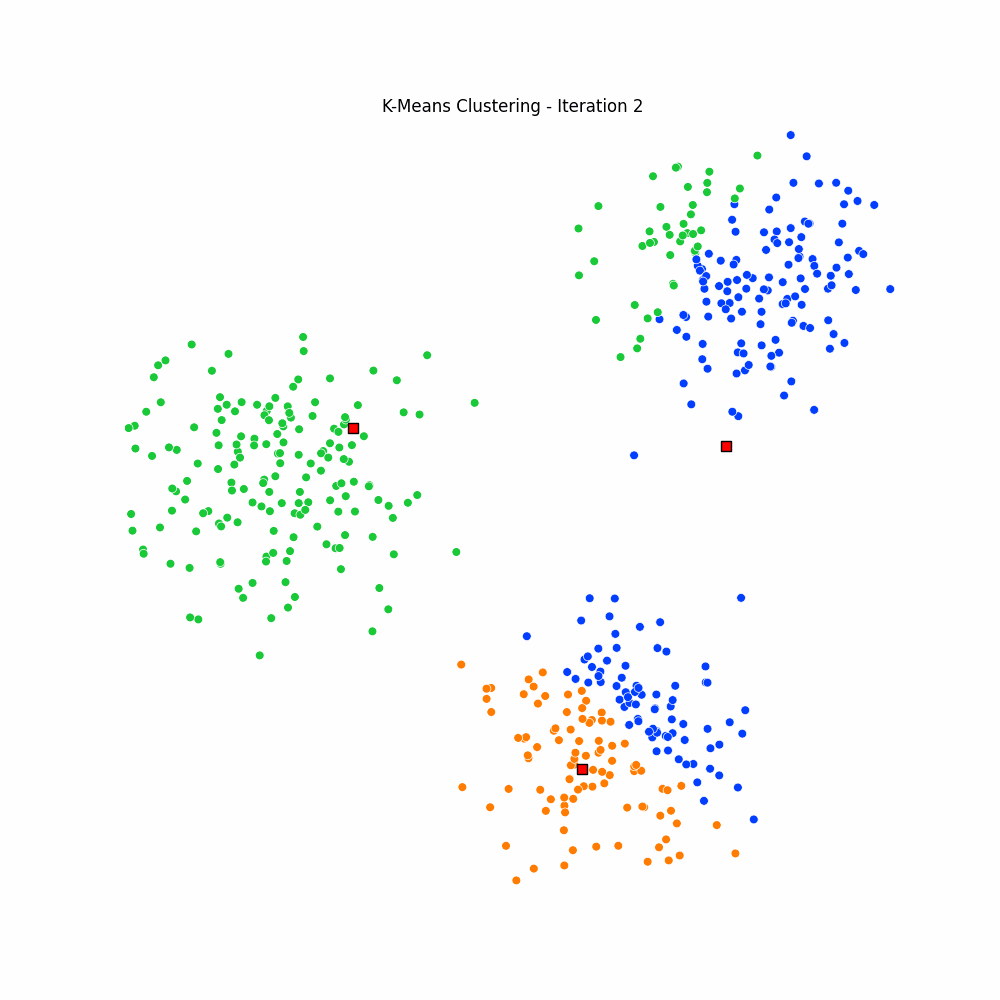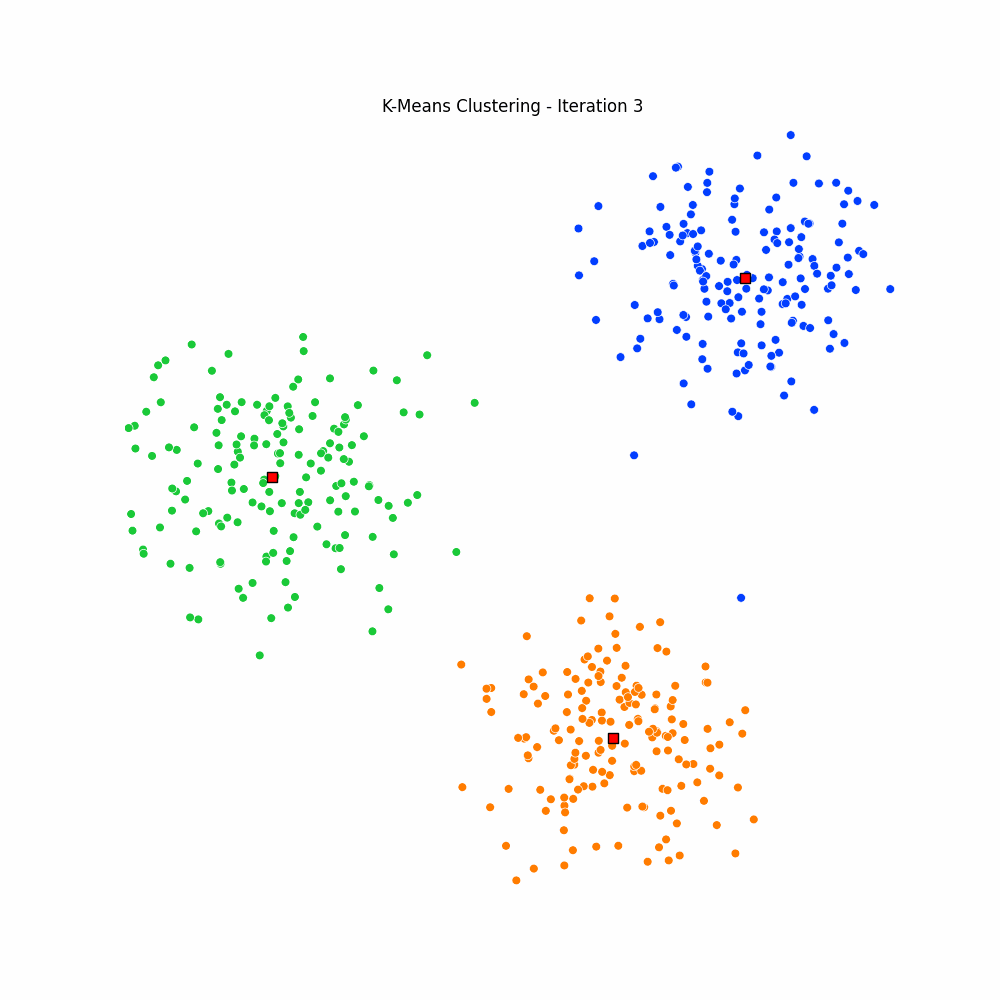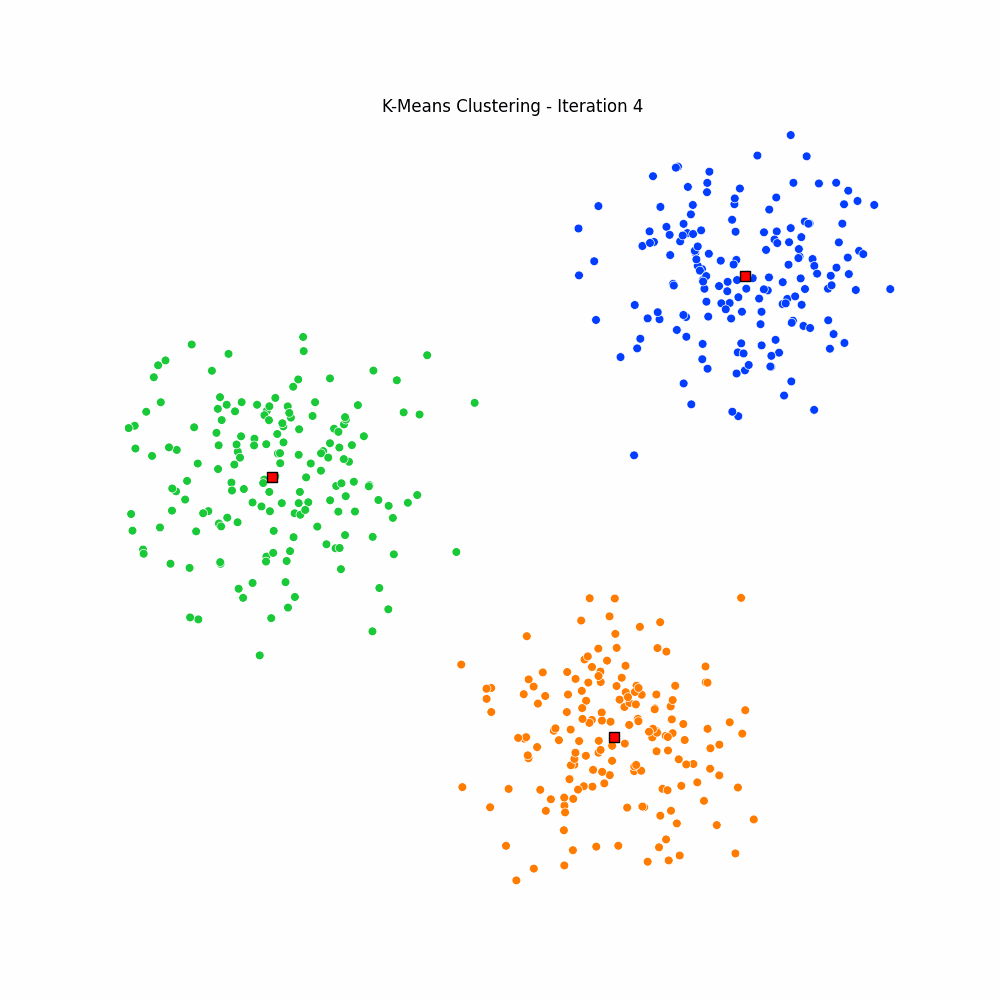
Animated gif of k-means clustering iterations.
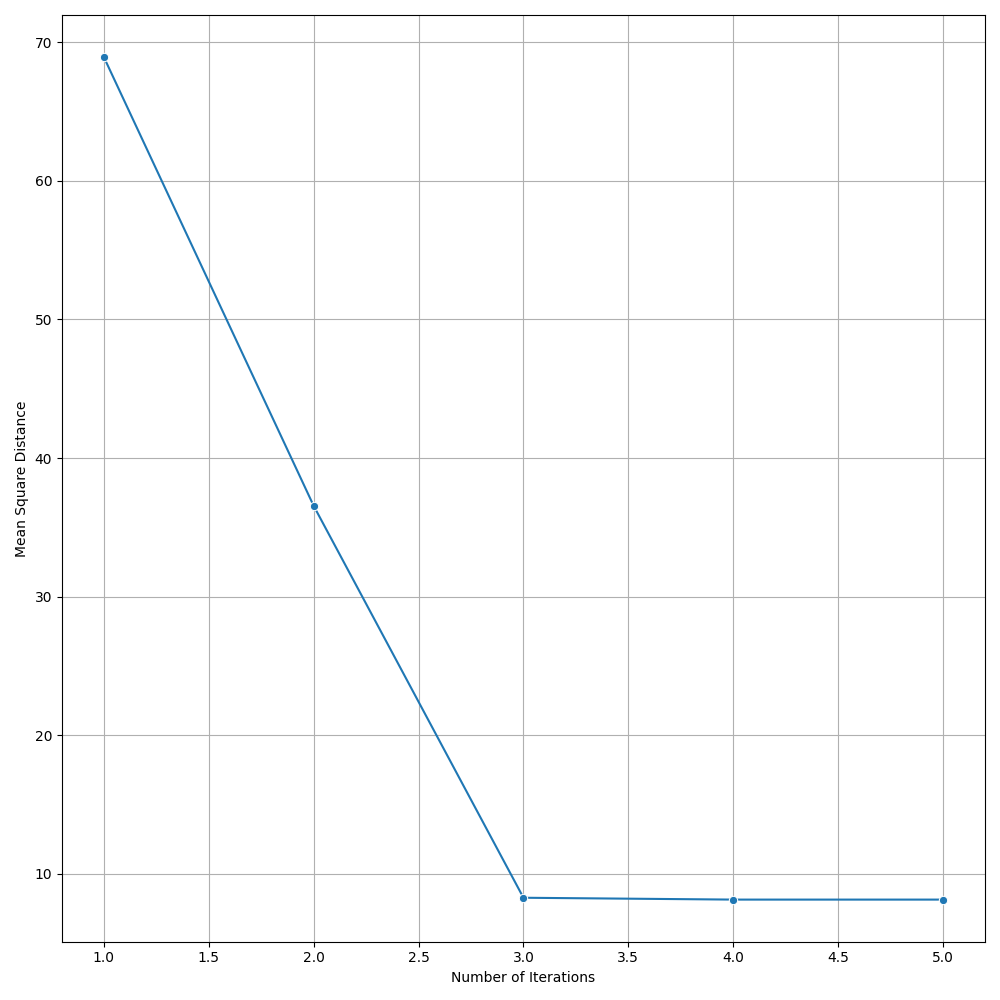
Iterations of k-means algorithm versus mean square distance.

Concluding thoughts

To conclude let us simply remind ourselves that clustering algorithms serve as foundational techniques across the domains data science, machine learning, and mathematics, offering a way to uncover inherent structures and patterns in data. We focused specifically on the k-means algorithm, it being one of the most popular unsupervised techniques available to the data science community. We then went on to discuss the many different applications of clustering, followed by a walkthrough of the algorithm for k-means. We finished with an animated gif of the iterative process behind k-means.

References